Creating Vertically Aligned Math Problems
Vertically aligned problems can be created by filling in entries in a borderless matrix. The example below will go over this process in more detail.
Vertically Aligned Multiplication Example
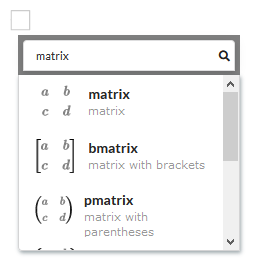
Let’s write out the multiplication problem 12 x 23 in a vertical format. Start by creating a borderless 3 x 3 matrix. Press the \ key to bring up the search bar and type matrix. Then choose the first option as shown below. When prompted to choose the number of rows and columns, choose 3 for both and click the Insert button.
Now, let’s being replacing the default 0 elements in the matrix with our given multiplication problem. In the first row, delete the 0 in the first column, replace the 0 in the second column with a 1, and replace the 0 in the third column with a 2.

Follow the same procedure to fill out the second row. This time, in the first column, delete the 0 and use the search menu to search for times which will give you the multiplication symbol. You can also insert this symbol from the menus at the top of the editor.
Next, we have to add a horizontal line under which we can write the result. We can do this by using matrix borders. Position the text cursor into the second row and click on the blue circular matrix menu icon on the bottom left of the editor. Navigate to the borders tab and choose the option in the bottom left indicating you want to add a horizontal border across the matrix underneath the current row. This menu can also be used to remove unwanted borders that appear above or below a certain row.

Before we write the answer, let’s show the intermediate steps. We can fill out the rows as we had before but notice that the matrix will run out of rows. To resolve this, new rows can easily be added by pressing the ENTER key or from the matrix menu. This menu can also be used to add new columns.
Using the methods described above, we can complete the vertically aligned multiplication problem as shown below.
